新闻列表

187 - 6397 - 2757
现如今,随着计算机科学技术的不断发展,信息技术与数学学科的结合也变得越来越紧密,在学习中,我们随处可见不会的数学题通过编程解答,我们的解题思路完全可以通过编程去实现它,让孩子在学习数学中不需要以“死记硬背”的学习方式去学习数学而是通过理解的方式去解决数学题,真正整整做到了让孩子“吃透数学“、”玩转数学”。接下来我们就要再一次验证,通过编程解决我们学科中的实际数学题!
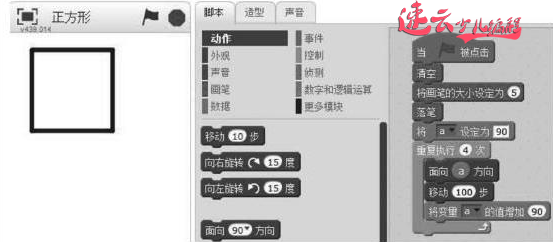
图一:绘制正方形

图二:绘制正十边形
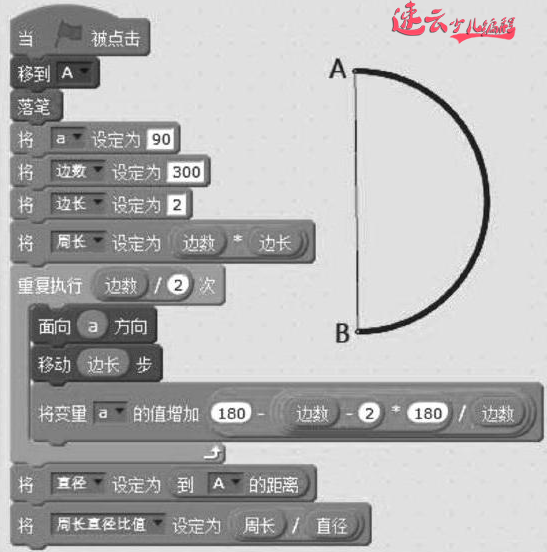
图三:求解圆周率
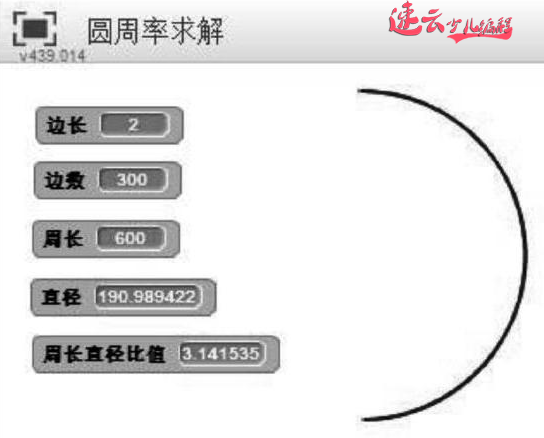
图四:运行结果

图五:

图六:

图七:
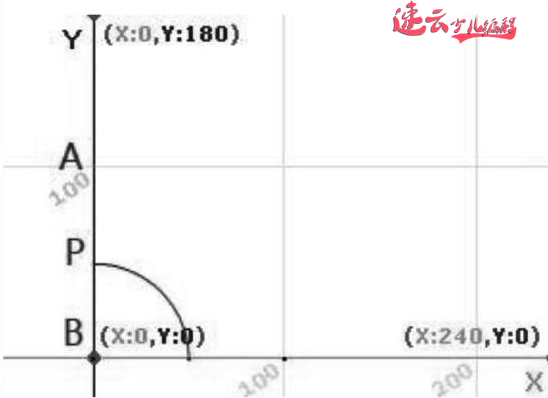
图八:
在一节数学课上,老师在讲到圆周率时告诉学生:圆周率是表示圆的周长与直径比值的数学常数,用希腊字母π表示。在公元480年左右,数学家祖冲之就得出精确到小数点后7位的结果,并给出不足近似值3.1415926和过剩近似值3.1415927,还得到两个近似分数值——密率 和约率 。但这个值是如何得来的呢?可以再精确些吗?古人的方法值得学习,那现代社会拥有发达的科学技术,我们可以用什么方法进行计算呢?在老师们抛出这个问题之后,学生们带着思考各自想办法并讨论,最后发现,这个问题我们居然可以在以前学习的编程上进行解答出来,接下来我们看吧!
1.分析问题
根据圆周长的计算公式可知,圆周率等于圆周长除以直径,所以,只要画一个任意的圆,然后测量出其周长及半径即可得到答案。由于圆周长是曲线,不易测量,用正n边形来代替圆,这样,就可以方便地得到圆周长,n越大,越接近圆,精确度也就越高。其中的难点是,如何制作正n边形以及如何测量直径。
2.具体步骤
第一步,绘制正n边形。
如何绘制正n边形呢?可以通过绘制正方形得到启发,先看如何绘制正方形。如图1,将一个点移动4次,每次向不同的方向移动100步,利用有限次循环,第一次90度,第二次180度,第三次270度,第四次360度,然后将其轨迹显示出来就得到了一个边长为100的正方形。
根据正方形的绘制方法,很容易扩展到正n边形的绘制,如图2所示,绘制正十边形,只要将边数设为10,a的值在每次循环后增加180-(边数-2)×180/边数即可。任意正多边形都可以绘制,只要改变边数即可。
第二步,求解圆周率。
有了正n边形,周长就可以计算了,接下来只需要计算直径就可以,那正多边形的直径如何求得?其实正多边形的直径就是正多边形最长的一条对角线,所以只要画出半个正多边形,然后连接AB两点,测出AB的距离就可以得到直径长度,然后便可得到圆周率的近似值了(如图3)。
当边数为300时,运行结果显示:圆周率约等于3.141535(如图4)。
不同的边数所得到的圆周率近似值也不同(如下表),从表中可以发现,边数越大,圆周率的测得值越精确。
问题的拓展——以点涉面,创新思维
圆周率的问题解决了,但我们的老师又提出新问题:请同学们想一想,除了圆周率的问题,还有哪些数学问题也可以运用程序去解决呢?由于程序可以测量两个点之间的距离,又可以绘制运动的轨迹,学生经过讨论发现很多数学问题都可以通过程序来解决。于是,“求动点的轨迹”的新的实践行动又一次展开了。
例题:1m长的木棍竖直紧贴墙壁,木棍滑落时,其中点的轨迹是什么?如果能想到直角三角形斜边中线定理,此题便迎刃而解,但如果想不到,就会变得很棘手。而运用程序来模拟木棍倒下的过程,就可以清晰地看到结论。用三个点分别代表木棍的两端和中点,在木棍滑落时,只要使两个端点始终保持固定长度,并且一个端点始终在Y轴上,另一个端点始终在X轴上就可以了。中点的坐标很容易获得,最终只要将中点的軌迹画出来便大功告成了。具体步骤:先画出三个点的角色,分别命名为A、B和P。设AB的距离为100,则AB两点的坐标分别为A(0,100),B(0,0),当按下空格键时,A点的X坐标不变,Y坐标不停地减小,而B点的Y坐标不变,X坐标不停地增大,具体可根据勾股定理获得相应的坐标。P点的坐标始终是AB两点的中点坐标,最后将P点的轨迹绘制出来,便可以看到是四分之一的圆弧。
图5~图8分别是A、B和P三点的脚本程序和运行结果。
问题的反思——计算思维的跨学科培养
2006年,美国卡内基·梅隆大学计算机科学系主任周以真教授提出,计算思维是运用计算机科学的基础概念进行问题求解、系统设计、以及人类行为理解等涵盖计算机科学之广度的一系列思维活动。同时又解释,这是一种采用抽象和分解来控制庞杂的任务或进行巨大复杂系统设计的方法;是通过约简、嵌入、转化和仿真等方法,把一个看来困难的问题重新阐释成一个我们知道问题怎样解决的方法等。华东师范大学王荣良教授也提出,“从计算思维教育的角度出发,其关键在于能对需要解决的问题进行抽象,形成计算机能够理解的形式化表达,并且让计算机自动地去计算。”那么本文例子中,哪些体现了计算思维的方法呢?
1.抽象的思维
科学的抽象是在概念中反映自然界或社会物质过程的内在本质的思想,它是在对事物的本质属性进行分析、综合、比较的基础上,抽取出事物的本质属性,撇开其非本质属性,使认识从感性的具体进入抽象的规定,形成概念。计算思维中的抽象,主要是指将现实生活中复杂难解的应用性问题,抽象成为可计算的问题。对于动点轨迹来讲,画出一根木棍,让它沿着墙壁慢慢倒下,这时,就可以利用抽象思维,将木棍看成三个点,即两个端点和一个中点。只要保证这三个点的相对距离不变,就可以模拟成一根木棍。
2.转化的思维
转化,是一种最基本的思维策略,更是一种有效的数学思维方式。所谓转化,就是在研究和解决有关问题时采用某种手段将问题通过变换使之转化,进而达到问题解决的一种方法。一般总是将复杂问题通过变换转化为简单问题,将难解的问题通过变换转化为容易求解的问题,将未解决的问题通过变换转化为已解决的问题。对于求解圆周率这个问题来讲,为了能得到一个圆的周长,把正n边形近似看作是一个圆(n越大,越接近于圆),这便是转化,转化后,根据周长公式得到了圆的周长。另外,为了得到一个正n边形,先从最简单的正方形入手,然后根据画正方形的方法推导出画正n边形的方法,这也是转化,是将复杂问题转化为简单问题。学生在编程过程中,自然而然就体会到了转化思维的好处。
3.自动化的思维
从某种程度上来说,自动化是计算机的工作。而执行此工作的前提则是需要将自然语言转换成为计算机可执行的语言。因此,编程在某种程度上成为自动化的替代。简言之,一个问题在经过转换后,需要执行与求解,因此需要将描述性问题中的自然语言转换为计算机语言,使问题得到充分解决,这就是自动化的过程。在第一个程序里,只要点击绿旗开始,并且输入边数和边长,系统便会得出结论,即周长与直径的比值,也就是圆周率。第二个程序开始后按下空格键,中点的轨迹便自动显示出来,一目了然。这些都蕴含着自动化的思维。
通过这次的“编程+数学”的实践,对学生而言,他们养成了爱探究、善分析、勤思考的学习品质。学生在学习中,扩散思维,找出用编程求解圆周率、发现动点运动轨迹的方法,找到了解決数学问题的途径,发现了编程的优势。学生在老师的启发下,仔细分析,拓展思路,寻找用编程解决其他的数学问题。
这个时候,家长们你还认为编程就是给孩子增加一个兴趣吗?



计算机是不是很强大呀!但前提是你要会编程呀!只有会编程,你才能让计算机替你解决问题呀!别担心,编程其实也没有想象那么难!只要你愿意学。


当然,无人机编程就更加深奥,比如我们看下面的视频吧!
无人机能六架一起起飞?没错!那他又和数学有什么关系呢?
小云说啦!这是根据我们数学中的坐标轴的 x轴 y轴 初始化无人机位置,无人机与无人机之间的距离、架数的多少,全部需要通过精密的计算,否则无法编排出理想的造型。
现在作为家长的你!还在纠结无人机编程是否对孩子有帮助吗?
无人机编程能做什么?人脸识别?智能跟随?自动飞行?还有吗?
答案:有!那就是"无人机编舞"!不知道无人机如何编舞?快看下面我们速云小童鞋的无人机编舞吧!!
无人机编程都学习哪些内容呢?
让无人机与编程结合?
没错!就是要让孩子“动手”+“编程”实现无人机起飞。
重点培养孩子逻辑思维能力与动手操作能力,让孩子在编写无人机程序的时,无形的锻炼孩子的逻辑思维能力和前沿科技的运用能力,在飞行学习中,孩子们需了解飞机的机械结构,练习手眼协同能力,甚至自己组装飞行器;在编程中,无人机可以在三维空间中,用摄像头完成巡线、人脸识别等人工智能任务。
例如:人脸识别,智能跟随,红外线定稿,光流定位、无人机编舞等。


看我们小童鞋们上课视频吧
坦克编程都学习哪些内容呢?
动手组装”+“编写程序”
通过编程将抽象理论与实践操作合二为一,让孩子重新理解知识,体验人工智能,培养独立思考的习惯和动手解决问题的能力。
课程涉及机器人拼装、力学等数理知识,运用六类人工智能模块,编写专属的自动驾驶算法程序,让孩子更加深入理解人工智能技术。
例如:人脸识别、智能跟随等前沿技术。

