新闻列表

187 - 6397 - 2757
在其他几篇文章中,同学们是否记得我们也做过一下古代数学题呀?比如“韩信点兵”、“李白沽酒”、“哪吒与夜叉”。
今天我们再来一道古代数学题“引葭赴岸”。
“引葭赴岸”问题,是我国数学经典著作《九章算术》中的一道名题。
原文:“今有池方一丈,葭生其中央。出水一尺,引葭赴岸,适与岸齐。问水深、葭长各几何。”
翻译:现有一水池一丈见方,池中生有一棵初生的芦苇,露出水面一尺,如把它引向岸边,正好与岸边齐平,问水有多深,该芦苇有多长?(一丈等于十尺)

这一问题在世界数学史上很有影响。印度古代数学家婆什迦罗的《丽罗瓦提》一书中有按这一问题改编的”风动红莲”;阿拉伯数学家阿尔•卡西的《算术之钥》也有类似的”池中长茅”问题;欧洲《十六世纪的算术》一书中又有”圆池芦苇”问题。它们比我国要晚几百上千年。
我们的老祖宗真是太有文采了,能用文言文准确描述数学概念。
这就是大家都知道的勾股定理,我们不妨用现代的解法把它解出来。
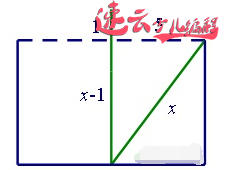
如图,设葭长为x丈,根据勾股定理有(x-1)²+5²=x²,解得x=13,故水深13-1=12丈,葭长13丈。
今天,我们不妨用Scratch来解一下这个古老的数学题,写出100以内所有的勾股数。
勾股数就是可以构成一个直角三角形三边的一组正整数。勾股定理:直角三角形两条直角边a、b的平方和等于斜边c的平方(a²+b²=c²)。
最小的勾股数是3、4、5。要避免3、4、5和4、3、5这样重复的勾股数,就要使三个数符合a<b<c的关系。该程序采用枚举算法,从3开始依次列举a、b、c三个变量的可能值,并使用勾股定理判断这三个变量值是否符合要求。如果符合勾股定理的要求,就把这三个变量记录到“勾股数”链表中。

编程过程如下:
先建立3个变量:
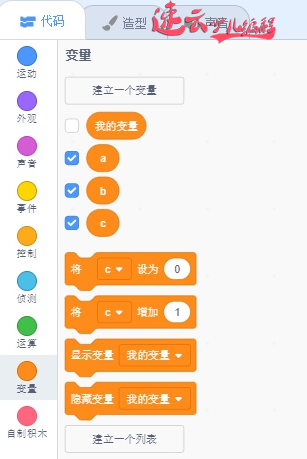
再建立一个列表,用于存放勾股数:
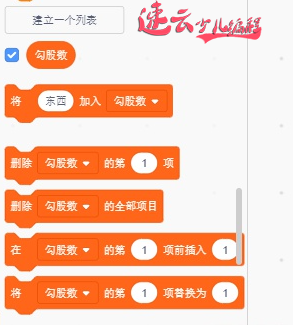
具体代码如下:
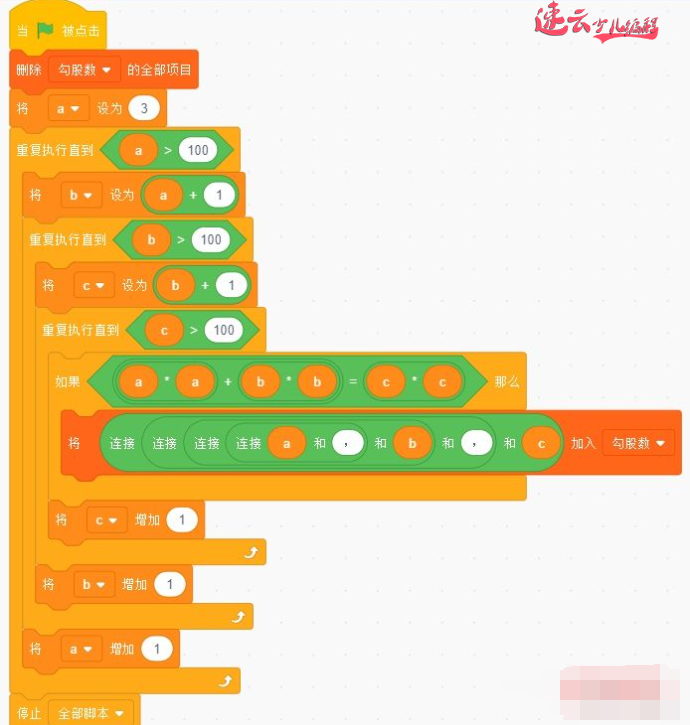
运行代码,将会得到100以内所有的勾股数,并记录到“勾股数”链表中。
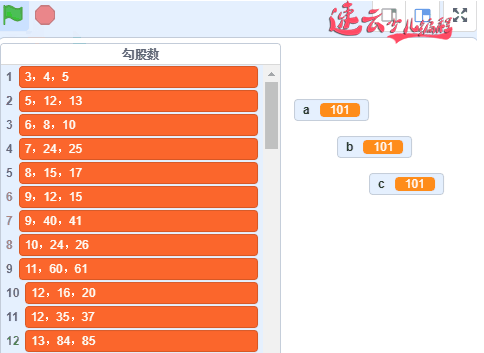
这个时候,家长们你还认为编程就是给孩子增加一个兴趣吗?



计算机是不是很强大呀!但前提是你要会编程呀!只有会编程,你才能让计算机替你解决问题呀!别担心,编程其实也没有想象那么难!只要你愿意学。


当然,无人机编程就更加深奥,比如我们看下面的视频吧!
无人机能六架一起起飞?没错!那他又和数学有什么关系呢?
小云说啦!这是根据我们数学中的坐标轴的 x轴 y轴 初始化无人机位置,无人机与无人机之间的距离、架数的多少,全部需要通过精密的计算,否则无法编排出理想的造型。
现在作为家长的你!还在纠结无人机编程是否对孩子有帮助吗?
无人机编程能做什么?人脸识别?智能跟随?自动飞行?还有吗?
答案:有!那就是"无人机编舞"!不知道无人机如何编舞?快看下面我们速云小童鞋的无人机编舞吧!!
无人机编程都学习哪些内容呢?
让无人机与编程结合?
没错!就是要让孩子“动手”+“编程”实现无人机起飞。
重点培养孩子逻辑思维能力与动手操作能力,让孩子在编写无人机程序的时,无形的锻炼孩子的逻辑思维能力和前沿科技的运用能力,在飞行学习中,孩子们需了解飞机的机械结构,练习手眼协同能力,甚至自己组装飞行器;在编程中,无人机可以在三维空间中,用摄像头完成巡线、人脸识别等人工智能任务。
例如:人脸识别,智能跟随,红外线定稿,光流定位、无人机编舞等。


看我们小童鞋们上课视频吧
坦克编程都学习哪些内容呢?
动手组装”+“编写程序”
通过编程将抽象理论与实践操作合二为一,让孩子重新理解知识,体验人工智能,培养独立思考的习惯和动手解决问题的能力。
课程涉及机器人拼装、力学等数理知识,运用六类人工智能模块,编写专属的自动驾驶算法程序,让孩子更加深入理解人工智能技术。
例如:人脸识别、智能跟随等前沿技术。

