新闻列表

187 - 6397 - 2757
大家好!小云老师又来了!在我们前几篇文章中,小云老师分别给各位家长讲解了,用编程实现“鸡兔同笼”、“韩信点兵”、“妇人洗碗”以及我们数学题中的“相遇问题”。也用编程带领同学们做了小游戏,比如“贪吃蛇”、“超级玛丽”、“坦克大战”,今天我们还用编程解题“求最大公约数”!可能经常关注我们“速云少儿编程”的家长们说了,前几篇文章涉足过“求最大公约数”,为什么还需要再讲一遍呢?因为今天的编程非“积木式Scratch”编程了,也就是我们传说中的信息学竞赛的编程“求最大公约数”。各位家长快看吧!

数学是计算机程序设计的灵魂。利用数学方面的知识、数学分析的方法以及数学题解的技巧,可以使得程序设计变得轻松、美观、高效,而且往往能反映出问题的本质。在各项程序设计比赛(比如,ACM、NOI)活动中,越来越多地用到各种复杂的数学知识,对选手的数学修养要求越来越高。今天奥而思燕老师就带大家来回顾一下信息学竞赛中考核到的数学相关基础知识之【最大公约数】
最大公约数
一般地,设a1,a2,a3…ak是k个非零整数,如果存在一个非零整数d,使得d|a1,d|a2,d|a3…"d|ak,那么d就称为a1,a2,a3…ak的公约数。公约数中最大的一个就称为最大公约数,记为GCD(a1,a2,a3…ak),显然它是存在的,至少为1。当GCD=1时,称这n个数是互质的或既约的。公约数一定是最大公约数的约数。
一般地,设a1,a2,a3,…ak是k个非零整数,如果存在一个非零整数d,使得a1|d,a2ld,a3ld,…ak|d,那么d就称为a1,a2,a3,…ak的公倍数。公倍数中最小的一个就称为最小公倍数,记为LCM(a1,a2,a3,…ak),显然它也是存在的。公倍数一定是最小公倍数的倍数。

辗转相除法
辗转相除法用来求两个数的最大公约数,又称欧几里得算法,其原理就是:GCD(x,y)=GCD(x,y-x)。
原理的证明如下:
设z|x,z|y,则z|(y-x)。
设z不是x的因子,则z不是x,y-x的公因子。
设z|x,z不是y的因子,则z不是x,y-x的公因子。
代码实现如下:
int GCD(int x, int y) {
return y==0? x: GCD(y, x%y);
}
二进制算法
如果想要进一步提高GCD的效率,可以通过不断去除因子2来降低常数,这就是所谓的“二进制算法”。
(1)若x,y均为偶数,则GCD(x,y)=2*GCD(x/2,y/2);
(2)若x为偶数,y为奇数,则GCD(x,y)=GCD(x/2,y);
(3)若x为奇数,y为偶数,则GCD(x,y)=GCD(x,y/2);
(4)若x,y均为奇数,则GCD(x,y)=GCD(x-y,y)。
代码实现如下:
inline int GCD(int x, int y){
int i,j;
if(x==0)return y;
if(y==0) return x;
for(i=0;0==(x&1);++i)x>>=1/去掉所有的2
for(j=0;0==(y&1);++j)y>>=1//去掉所有的2
while(1){
If(x<y)x^=y,y^=x,x^=Y;/若x<y交换x,y
if(0==(x-=y)) return y<<i;< p="">
//若x==y,gcd==x==y(就是在辗转减, while(1)控制)
while(0==(x&1)x>>=1;/去掉所有的2
最小公倍数
求两个数的最小公倍数可以使用“逐步倍增”法,如求3和8的最小公倍数,可以让n从1开始逐步加1,不断检查8*n是不是3的倍数,直到n=3时,8*3=24是3的倍数了,还可以直接使用以下定理来求解。
定理:a、b两个数的最大公约数乘以它们的最小公倍数就等于a和b本身的乘积。
比如,要求3和8的最小公倍数,则LCM(3,8)=3*8 div GCD(3,8)=24
扩展欧几里得算法
扩展欧几里德算法是用来在已知(a,b)时,求解一组(p,q),使得 p*a+q*b=GCD(a,b)。
首先,根据数论中的相关定理,解一定存在。
其次,因为GCD(a,b)= GCD(b,a%b),所以p*a+q*b=GCD(a,b)= GCD(b,a%b)=p*b+q*a%b=p*b+q*(a-a/b*b)=q*a+(P-a/b*q)*b,这样它就将a 与b的线性组合化简为b与a %b的线性组合。
根据前边的结论:a和b都在减小,当b减小到0时,就可以得出p=1,q=0。然后递归回去就可以求出最终的p和q了。
代码实现如下:
#include< stdio.h> //形如ax+by=GCD(a,b)
int extended _gcd(int a, int b, int &x, int &y){
int ret, tmp;
if ( !b)(
x=1;
y=0;
return a;
}
ret-extended_gcd(b, a% b, x, y);
tmp = x;
x=y;
y= tmp-a/b * y;
return ret;
}
int main() {
Int a, b, x, y, z;
scanf(“%d%d”,&a, &b);
z= extended_ gcd(a, b, x, y);
printf("%d%d%dn",z,x,y);
return 0;
}
求解线性同余方程
定理1:对于方程a*x+b*y=c,该方程等价于a*x=c(mod b),有整数解的充分必要条件是:c%GCD(a,b)=0。
根据定理1,对于方程a*x+b*y=c,我们可以先用扩展欧几里德算法求出一组x0,y0,也就是a*x0+b*y0=GCD(a,b),然后两边同时除以GCD(a,b),再乘以c。这样就得到了方程 a*x0*c/GCD(a,b)+b*y0*c/GCD(a,b)=c,我们也就找到了方程的一个解
定理2:若GCD(a,b)=1,且x0,y0为a*x+b*y=c的一组解,则该方程的任一解可表示为:x=x0+b*t,y=y0-a*t,且对任一整数,皆成立。
根据定理2,可以求出方程的所有解。但实际问题中,我们往往被要求去最小整数解,也就是求一个特解x,t= b/GCD(a,b),x=(x%t+t)%t。
代码实现如下:
int Extended_Euclid(int a, int b, int& x, int &y)(
if(b==0){
x=1 ;
y=0 ;
return a;
}
int d=Extended_Euclid(b, a %b, x, y);
int temp =x ; x=y ; y=temp-a/b*y;
return d;
}
//用扩展欧几里得算法解线性方程ax+by=c;
bool linearEquation(int a, int b, int c, int& x, int &y){
int d= Extended_Euclid(a, b, x, y);
if(c%d) return false;
int k=c/d;
x*=k;//+t*b;
y*=k;//-t*a;
//求的只是其中一个解
速云少儿编程致力于 4 - 18 岁,山东少儿无人机编程教育机构,教给孩子们不光要学习编程,还要结合编程知识给我们无人机写程序,实现我们无人机的自动启飞、人脸识别、智能跟随,包括更加高级的编程玩法,就是无人机编舞。可能家长想了!四岁孩子能学习无人机编程吗?那我们看个四岁的小同学吧,你自己看看能不能学习吧!
我们来看一看四岁小朋友的学习视频吧!
家长担心孩子们真的能听懂课程吗?在每节课即将结束的时候我们都会进行课程汇报展示,来看一下小童鞋的汇报成果吧!
这个时候家长可能说了,我们四岁的孩子,年龄辣么小,又不认字,那该如何学习呢?
其实四岁、五岁的孩子不认字怎么学习?只要孩子识别颜色就可以学习。通过颜色识别具体编程积木,比如:蓝色是运动、紫色是外观、黄色是事件等等,通过颜色识别文字,根据颜色先实现出程序做出卡通的效果,以激发孩子兴趣,使孩子产生兴趣后开始具体学习每个积木的作用,再学习积木上面的文字。如下图:
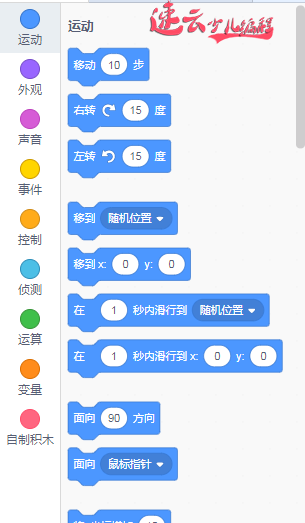
这个时候你还认为编程难吗?其实针对4岁起,就已经可以学习编程了。通过搭积木的方式让孩子学习编程。
当然,比如我们下面的无人机编程视频吧!
无人机能六架一起起飞?没错!那他又和数学有什么关系呢?
小云说啦!这是根据我们数学中的坐标轴的 x轴 y轴 初始化无人机位置,无人机与无人机之间的距离、架数的多少,全部需要通过精密的计算,否则无法编排出理想的造型。
现在作为家长的你!还在纠结无人机编程是否对孩子有帮助吗?
无人机编程能做什么?人脸识别?智能跟随?自动飞行?还有吗?
答案:有!那就是"无人机编舞"!不知道无人机如何编舞?快看下面我们速云小童鞋的无人机编舞吧!!
无人机编程都学习哪些内容呢?
让无人机与编程结合?
没错!就是要让孩子“动手”+“编程”实现无人机起飞。
重点培养孩子逻辑思维能力与动手操作能力,让孩子在编写无人机程序的时,无形的锻炼孩子的逻辑思维能力和前沿科技的运用能力,在飞行学习中,孩子们需了解飞机的机械结构,练习手眼协同能力,甚至自己组装飞行器;在编程中,无人机可以在三维空间中,用摄像头完成巡线、人脸识别等人工智能任务。
例如:人脸识别,智能跟随,红外线定稿,光流定位、无人机编舞等。


看我们小童鞋们上课视频吧
坦克编程都学习哪些内容呢?
动手组装”+“编写程序”
通过编程将抽象理论与实践操作合二为一,让孩子重新理解知识,体验人工智能,培养独立思考的习惯和动手解决问题的能力。
课程涉及机器人拼装、力学等数理知识,运用六类人工智能模块,编写专属的自动驾驶算法程序,让孩子更加深入理解人工智能技术。
例如:人脸识别、智能跟随等前沿技术。

